Using Trigonometry and Pythagoras to WaterMark an Image

Introduction

The class presented here will place a watermark on an image. It takes a Bitmap object and returns anotherBitmap with a string drawn diagonally (top-left to bottom-right) across it. An instance of the class is constructed with the actual text to place, font properties, maximum wanted font size (more on this in a bit),Color and transparency (byte).

This may sound fairly trivial but calculating the angle of the diagonal line through a Rectangle of unknown Size at design time (big d'oh! if there's a library method that already does this!) and autosizing the font to fill as much of the bitmap as possible, without being clipped involves Trigonometry and Pythagoras. This is what I aim to show here.

Background

I answered this question in the C# forum with a quick and dirty answer. The original poster seemed happy with my answer but I was spurred on to make it better.

I have done a bit of development on image filters before and have modeled my class structure based on this article, by Andrew Kirillov (recommended reading if you are interested in learning about GDI+). The class in my article also uses this structure. I have, however, removed the IFilter interface for the purpose of this article as I am only covering 1 class and it would detract from the focus (if you don't know what I mean by that last sentence then forget I said anything, it doesn't matter :) ).

I am a tester by trade but I have taught myself C# over the course of the last 3 years. The way I have solved the problem here may not be the quickest, easiest or optimum approach. I just used my current knowledge of C# and tried to remember my school Trigonometry and Pythagoras as best I could. I'm sure there are ways for further improvement. A couple of ideas that come to mind is an enum to select which way to draw the watermark (eg diagonally-down, diagonally-up, horizontal etc) or being able to handle multiple lines of text. Any comments or suggestions for improvement are most welcome.

Using the code

I decided to solve this problem by breaking it down into bite size pieces, solving each part separately and building up my class progressively.

1. Draw a string on an image

The starting point. Below is the basic structure of the class which draws the supplied string to the Bitmapobject. Simply placed at 0,0 with no fancy transparency, angles or resizing.

 Collapse | Copy Code

using System;
using System.Drawing;
using System.Drawing.Drawing2D;

namespace DM.Imaging
{
   public class WaterMark
   {
      private string waterMarkText;
      private string fontName;
      private FontStyle fontStyle;
      private Color color;
      private int fontSize;

      public WaterMark(string waterMarkText, 
                       string fontName, int fontSize,
                       FontStyle fontStyle, Color color)
      {
         this.waterMarkText = waterMarkText;
         this.fontName = fontName;
         this.fontStyle = fontStyle;
         this.color = color;
         this.fontSize = fontSize;
      }

      public Bitmap Apply(Bitmap bitmap)
      {
         Bitmap newBitmap = new Bitmap(bitmap);
         Graphics g = Graphics.FromImage(newBitmap);

         Font font = new Font(fontName, fontSize, 
                              fontStyle);

         g.DrawString(waterMarkText, font,  
                      new SolidBrush(color), new Point(
                      0, 0));

         return newBitmap;
      }
   }
}

This is a simplification of what it produces:

2. Place string diagonally

Ok, so now I need to calculate the angle. Here we use a bit of Trigonometry. Remember SOHCAHTOA? If we draw an imaginary diagonal line through our bitmap then we end up with a right-angled triangle:

By the basic rules of Trigonometry we can calculate the tangent of the angle by dividing the length of the opposite side by the length of the adjacent side. In this case, dividing the bitmap's height by its width:

 Collapse | Copy Code

double tangent = (double)newBitmap.Height / 
                 (double)newBitmap.Width;

We can then calculate the angle from it's tangent by using the Math.Atan method, like so:

 Collapse | Copy Code

double angle = Math.Atan(tangent) * (180 / Math.PI);

All we need to do now is apply this angle to our Graphics object before we draw the string:

 Collapse | Copy Code

g.RotateTransform((float)angle);

This is just about where we've got:

3. Draw the string in the middle

Now I need to move the string so that it is drawn dead-centre of the bitmap. Therefore, we need to draw the string half way along our diagonal line. This is where Pythagoras comes in. If we go back to our imaginary triangle, we will see that we can calculate the length of the diagonal line, or the hypotenuse, by the formula a^2 = b^2 + c^2 or a = sqrt(b^2 + c^2).

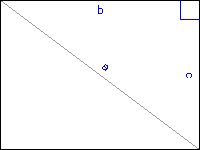
This will translate to:

 Collapse | Copy Code

double halfHypotenuse = Math.Sqrt((newBitmap.Height * 
       newBitmap.Height) + (newBitmap.Width * 
       newBitmap.Width)) / 2;            

All we need to do then is tweak the DrawString method to adjust the position of the string:

 Collapse | Copy Code

g.DrawString(waterMarkText, font, new SolidBrush(color), 
             new Point((int)halfHypotenuse, 0));

We're getting closer, but still not right:

4. Centre the string

The string is being drawn, by default, from the top-left of the Point we specify in the DrawString method. We can change this to the centre of the string by simple creating a StringFormat object, setting its alignment properties:

 Collapse | Copy Code

StringFormat stringFormat = new StringFormat();
stringFormat.Alignment = StringAlignment.Center;
stringFormat.LineAlignment = StringAlignment.Center;

...and adding this to the DrawString method, as this method has another overload which takes this as a parameter:

 Collapse | Copy Code

g.DrawString(waterMarkText, font, new SolidBrush(color), 
           new Point((int)halfHypotenuse, 0),stringFormat);

This is starting to look more like it:

5. Autoresize string

Have I bored you to death or are you still with me? If you're not asleep now, you will be after this section! Now, I want the user to be able to select a font size. But, if the size they select would clip some of the text (ie some of the string is drawn off the edge of the bitmap) then I want to automatically shrink the font so that it does fit.

If we imagine what a string that is too big will look like on the bitmap, and draw a rectangle around it. Then we see that we need to compare this imaginary (blue) rectangle with the bitmap dimensions. If the blue rectangle is bigger than the bitmap, then we know that we need to shrink the font, and check the again:

The hard part is calculating the Size of this imaginary blue rectangle. Firstly, we can measure how big the string will be by calling the Graphics.MeasureString method:

 Collapse | Copy Code

SizeF sizef = g.MeasureString(waterMarkText, font, 
                              int.MaxValue);

Now we have this, if we look at the picture in my head again, we see that we can split the blue rectangle up into triangles and split both the width and height into two Trig calculations (4 total) that we sum to give us the overall size. We already have the angle from our calculations before and we now know the hypotenuse for both the little and big triangles (sizef.Height and sizef.Width respectively):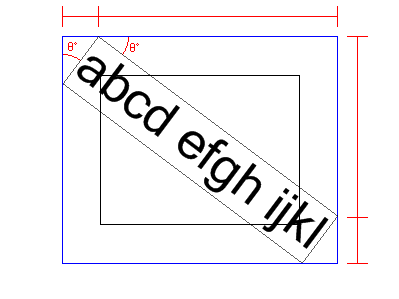

If we take the width of the big blue triangle first. To start, if we look at the smaller triangle we need to calculate the length of the side which is opposite to the angle we know and we have the hypotenuse. Using trig (sine) we can calculate this as follows:

 Collapse | Copy Code

double sin = Math.Sin(angle * (Math.PI / 180));
double opp1 = sin * sizef.Height;

If we repeat this methodology for the large triangle... We need to calculate the length of the side which is adjacent to the angle we know and we have the hypotenuse. This will be a cosine calculation:

 Collapse | Copy Code

double cos = Math.Cos(angle * (Math.PI / 180));
double adj1 = cos * sizef.Width;

We then just sum opp1 and adj1 to get the width. We repeat this for the height. At the end we check if the blue rectangle is smaller than the bitmap. If it isn't then we shrink the font down a bit and repeat the check. Once the string fits then we are good to go.

It may have been wiser to pull these statements out into their own method as using a break; in a for loop seems a bit dirty to me. But it works! So I'm not complaining. Here's the complete for loop:

 Collapse | Copy Code

Font font = new Font(fontName, maxFontSize, fontStyle);
for (int i = maxFontSize; i > 0; i--)
{
   font = new Font(fontName, i, fontStyle);
   SizeF sizef = g.MeasureString(waterMarkText, font, 
                                 int.MaxValue);

   double sin = Math.Sin(angle * (Math.PI / 180));
   double cos = Math.Cos(angle * (Math.PI / 180));

   double opp1 = sin * sizef.Height;
   double adj1 = cos * sizef.Width;

   double opp2 = sin * sizef.Width;
   double adj2 = cos * sizef.Height;

   if (opp1 + adj1 < newBitmap.Width &&
       opp2 + adj2 < newBitmap.Height)
   {
      break;
   }
}

Here a recap on where we're up to:

6. Make transparent and Antialias

We're on the home straight now. My head's beginning to hurt! All there is left to do is add the finishing touches. Drawing text at a rotated angle can look a bit, let's say, wrong. so it can't hurt to add some Antialias:

 Collapse | Copy Code

g.SmoothingMode = SmoothingMode.AntiAlias;

Transparency is added by changing the alpha level of the color, with 0 = invisible up to 255 = opaque.

 Collapse | Copy Code

public WaterMark(string waterMarkText, string fontName, 
                 int maxFontSize, FontStyle fontStyle, 
                 Color color, byte alpha)
{
   // ...
   this.color = Color.FromArgb(alpha, color);
}

And the finished result:

Well, that's it. Done. Here's the entire class:

 Collapse | Copy Code

using System;
using System.Drawing;
using System.Drawing.Drawing2D;

namespace DM.Imaging
{
   public class WaterMark
   {
      private string waterMarkText;
      private string fontName;
      private FontStyle fontStyle;
      private Color color;
      private int maxFontSize;

      public WaterMark(string waterMarkText, 
                       string fontName, int maxFontSize,
                       FontStyle fontStyle, Color color, 
                       byte alpha)
      {
         this.waterMarkText = waterMarkText;
         this.fontName = fontName;
         this.fontStyle = fontStyle;
         this.color = Color.FromArgb(alpha, color);
         this.maxFontSize = maxFontSize;
      }

      public Bitmap Apply(Bitmap bitmap)
      {
         Bitmap newBitmap = new Bitmap(bitmap);
         Graphics g = Graphics.FromImage(newBitmap);

         // Trigonometry: Tangent = Opposite / Adjacent
         // Remember SOHCAHTOA?
         double tangent = (double)newBitmap.Height / 
                          (double)newBitmap.Width;

         // convert arctangent to degrees
         double angle = Math.Atan(tangent) * (180/Math.PI);

         // Pythagoras here :-/
         // a^2 = b^2 + c^2 ; a = sqrt(b^2 + c^2)
         double halfHypotenuse =Math.Sqrt((newBitmap.Height 
                                * newBitmap.Height) +
                                (newBitmap.Width * 
                                newBitmap.Width)) / 2;

         // Horizontally and vertically aligned the string
         // This makes the placement Point the physical 
         // center of the string instead of top-left.
         StringFormat stringFormat = new StringFormat();
         stringFormat.Alignment = StringAlignment.Center;
         stringFormat.LineAlignment=StringAlignment.Center;

         // Calculate the size of the string (Graphics
         // .MeasureString)
         // and see if it fits in the bitmap completely. 
         // If it doesn’t, strink the font and check 
         // again... and again until it does fit.
         Font font = new Font(fontName,maxFontSize,
                              fontStyle);
         for (int i = maxFontSize; i > 0; i--)
         {
            font = new Font(fontName, i, fontStyle);
            SizeF sizef = g.MeasureString(waterMarkText, 
                           font, int.MaxValue);

            double sin = Math.Sin(angle * (Math.PI / 180));
            double cos = Math.Cos(angle * (Math.PI / 180));

            double opp1 = sin * sizef.Width;
            double adj1 = cos * sizef.Height;

            double opp2 = sin * sizef.Height;
            double adj2 = cos * sizef.Width;

            if (opp1 + adj1 < newBitmap.Height &&
                opp2 + adj2 < newBitmap.Width)
            {
               break;
            }
         }
         
         g.SmoothingMode = SmoothingMode.AntiAlias;
         g.RotateTransform((float)angle);            
         g.DrawString(waterMarkText, font, 
                      new SolidBrush(color),
                      new Point((int)halfHypotenuse, 0), 
                      stringFormat);

         return newBitmap;
      }
   }
}

Using the sample project

It should be fairly straight forward to see what's happening. Try resizing the form to see the watermark be updated on the fly.